Profile

We present a strongly coupled method for the robust simulation of linear magnetic rigid bodies. Our approach describes the magnetic effects as part of an incremental potential function. This potential is inserted into the reformulation of the equations of motion for rigid bodies as an optimization problem. For handling collision and friction, we lean on the Incremental Potential Contact (IPC) method. Furthermore, we provide a novel, hybrid explicit / implicit time integration scheme for the magnetic potential based on a distance criterion. This reduces the fill-in of the energy Hessian in cases where the change in magnetic potential energy is small, leading to a simulation speedup without compromising the stability of the system. The resulting system yields a strongly coupled method for the robust simulation of magnetic effects. We showcase the robustness in theory by analyzing the behavior of the magnetic attraction against the contact resolution. Furthermore, we display stability in practice by simulating exceedingly strong and arbitrarily shaped magnets. The results are free of artifacts like bouncing for time step sizes larger than with the equivalent weakly coupled approach. Finally, we showcase the utility of our method in different scenarios with complex joints and numerous magnets.

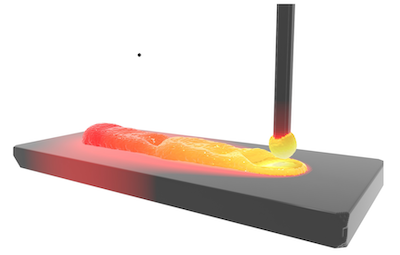
Cold metal transfer (CMT) is a variant of gas metal arc welding (GMAW) in which the molten metal of the wire is transferred to the weld pool mainly in the short-circuit phase. A special feature here is that the wire is retracted during this strongly controlled welding process. This allows precise and spatter-free formation of the weld seams with lower energy input. To simulate this process, a model based on the particle-based smoothed particle hydrodynamics (SPH) method is developed. This method provides a native solution for the mass and heat transfer. A simplified surrogate model was implemented as an arc heat source for welding simulation. This welding simulation model based on smoothed particle hydrodynamics method was augmented with surface effects, the Joule heating of the wire, and the effect of the electromagnetic forces. The model of metal transfer in the cold metal transfer process shows good qualitative agreement with real experiments.

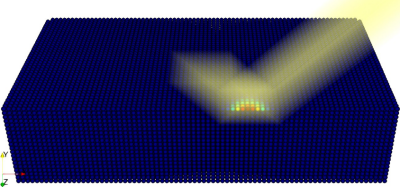
An important prerequisite for process simulations of laser beam welding is the accurate depiction of the surface energy distribution. This requires capturing the optical effects of the laser beam occurring at the free surface. In this work, a novel optics ray tracing scheme is proposed which can handle the reflection and absorption dynamics associated with laser beam welding. Showcasing the applicability of the approach, it is coupled with a novel surface detection algorithm based on smoothed particle hydrodynamics (SPH), which offers significant performance benefits over reconstruction-based methods. The results are compared to state-of-the-art experimental results in laser beam welding, for which an excellent correspondence in the case of the energy distributions inside capillaries is shown.

The numerical simulation of surface tension is an active area of research in many different fields of application and has been attempted using a wide range of methods. Our contribution is the derivation and implementation of an implicit cohesion force based approach for the simulation of surface tension effects using the Smoothed Particle Hydrodynamics (SPH) method. We define a continuous formulation inspired by the properties of surface tension at the molecular scale which is spatially discretized using SPH. An adapted variant of the linearized backward Euler method is used for time discretization, which we also strongly couple with an implicit viscosity model. Finally, we extend our formulation with adhesion forces for interfaces with rigid objects.

Existing SPH approaches for surface tension in computer graphics are mostly based on explicit time integration, thereby lacking in stability for challenging settings. We compare our implicit surface tension method to these approaches and further evaluate our model on a wider variety of complex scenarios, showcasing its efficacy and versatility. Among others, these include but are not limited to simulations of a water crown, a dripping faucet and a droplet-toy.

Paper (ACM, Free of Charge)

A well-known issue with the widely used Smoothed Particle Hydrodynamics (SPH) method is the neighborhood deficiency. Near the surface, the SPH interpolant fails to accurately capture the underlying fields due to a lack of neighboring particles. These errors may introduce ghost forces or other visual artifacts into the simulation.

In this work we investigate three different popular methods to correct the first-order spatial derivative SPH operators up to linear accuracy, namely the Kernel Gradient Correction (KGC), Moving Least Squares (MLS) and Reproducing Kernel Particle Method (RKPM). We provide a thorough, theoretical comparison in which we remark strong resemblance between the aforementioned methods. We support this by an analysis using synthetic test scenarios. Additionally, we apply the correction methods in simulations with boundary handling, viscosity, surface tension, vorticity and elastic solids to showcase the reduction or elimination of common numerical artifacts like ghost forces. Lastly, we show that incorporating the correction algorithms in a state-of-the-art SPH solver only incurs a negligible reduction in computational performance.

A common way to handle boundaries in SPH fluid simulations is to sample the surface of the boundary geometry using particles. These boundary particles are assigned the same properties as the fluid particles and are considered in the pressure force computation to avoid a penetration of the boundary. However, the pressure solver requires a pressure value for each particle. These are typically not computed for the boundary particles due to the computational overhead. Therefore, several strategies have been investigated in previous works to obtain boundary pressure values. A popular, simple technique is pressure mirroring, which mirrors the values from the fluid particles. This method is efficient, but may cause visual artifacts. More complex approaches like pressure extrapolation aim to avoid these artifacts at the cost of computation time.

We introduce a constraint-based derivation of Divergence-Free SPH (DFSPH) --- a common state-of-the-art pressure solver. This derivation gives us new insights on how to integrate boundary particles in the pressure solve without the need of explicitly computing boundary pressure values. This yields a more elegant formulation of the pressure solver that avoids the aforementioned problems.

We present a new octree-based neighborhood search method for SPH simulation. A speedup of up to 1.9x is observed in comparison to state-of-the-art methods which rely on uniform grids. While our method focuses on maximizing performance in fixed-radius SPH simulations, we show that it can also be used in scenarios where the particle support radius is not constant thanks to the adaptive nature of the octree acceleration structure.

Neighborhood search methods typically consist of an acceleration structure that prunes the space of possible particle neighbor pairs, followed by direct distance comparisons between the remaining particle pairs. Previous works have focused on minimizing the number of comparisons. However, in an effort to minimize the actual computation time, we find that distance comparisons exhibit very high throughput on modern CPUs. By permitting more comparisons than strictly necessary, the time spent on preparing and searching the acceleration structure can be reduced, yielding a net positive speedup. The choice of an octree acceleration structure, instead of the uniform grid typically used in fixed-radius methods, ensures balanced computational tasks. This benefits both parallelism and provides consistently high computational intensity for the distance comparisons. We present a detailed account of high-level considerations that, together with low-level decisions, enable high throughput for performance-critical parts of the algorithm.

Finally, we demonstrate the high performance of our algorithm on a number of large-scale fixed-radius SPH benchmarks and show in experiments with a support radius ratio up to 3 that our method is also effective in multi-resolution SPH simulations.