Publications

The use of simulation in robotics is increasingly widespread for the purpose of testing, synthetic data generation and skill learning. A relevant aspect of simulation for a variety of robot applications is physics-based simulation of robot-object interactions. This involves the challenge of accurately modeling and implementing different mechanical systems such as rigid and deformable bodies as well as their interactions via constraints, contact or friction. Most state-of-the-art physics engines commonly used in robotics either cannot couple deformable and rigid bodies in the same framework, lack important systems such as cloth or shells, have stability issues in complex friction-dominated setups or cannot robustly prevent penetrations. In this paper, we propose a framework for strongly coupled simulation of rigid and deformable bodies with focus on usability, stability, robustness and easy access to state-of-the-art deformation and frictional contact models. Our system uses the Finite Element Method (FEM) to model deformable solids, the Incremental Potential Contact (IPC) approach for frictional contact and a robust second order optimizer to ensure stable and penetration-free solutions to tight tolerances. It is a general purpose framework, not tied to a particular use case such as grasping or learning, it is written in C++ and comes with a Python interface. We demonstrate our system’s ability to reproduce complex real-world experiments where a mobile vacuum robot interacts with a towel on different floor types and towel geometries. Our system is able to reproduce 100% of the qualitative outcomes observed in the laboratory environment. The simulation pipeline, named Stark (the German word for strong, as in strong coupling) is made open-source.

Dynamics simulation with frictional contacts is important for a wide range of applications, from cloth simulation to object manipulation. Recent methods using smoothed lagged friction forces have enabled robust and differentiable simulation of elastodynamics with friction. However, the resulting frictional behavior can be inaccurate and may not converge to analytic solutions. Here we evaluate the accuracy of lagged friction models in comparison with implicit frictional contact systems. We show that major inaccuracies near the stick-slip threshold in such systems are caused by lagging of friction forces rather than by smoothing the Coulomb friction curve. Furthermore, we demonstrate how systems involving implicit or lagged friction can be correctly used with higher-order time integration and highlight limitations in earlier attempts. We demonstrate how to exploit forward-mode automatic differentiation to simplify and, in some cases, improve the performance of the inexact Newton method. Finally, we show that other complex phenomena can also be simulated effectively while maintaining smoothness of the entire system. We extend our method to exhibit stick-slip frictional behavior and preserve volume on compressible and nearly-incompressible media using soft constraints.

We present a strongly coupled method for the robust simulation of linear magnetic rigid bodies. Our approach describes the magnetic effects as part of an incremental potential function. This potential is inserted into the reformulation of the equations of motion for rigid bodies as an optimization problem. For handling collision and friction, we lean on the Incremental Potential Contact (IPC) method. Furthermore, we provide a novel, hybrid explicit / implicit time integration scheme for the magnetic potential based on a distance criterion. This reduces the fill-in of the energy Hessian in cases where the change in magnetic potential energy is small, leading to a simulation speedup without compromising the stability of the system. The resulting system yields a strongly coupled method for the robust simulation of magnetic effects. We showcase the robustness in theory by analyzing the behavior of the magnetic attraction against the contact resolution. Furthermore, we display stability in practice by simulating exceedingly strong and arbitrarily shaped magnets. The results are free of artifacts like bouncing for time step sizes larger than with the equivalent weakly coupled approach. Finally, we showcase the utility of our method in different scenarios with complex joints and numerous magnets.

Continuum-based shell models are an established approach for the simulation of thin deformables in computer graphics. However, existing research in physically-based animation is mostly focused on shear-rigid Kirchhoff-Love shells. In this work we explore three-director Cosserat (micropolar) shells which introduce additional rotational degrees of freedom. This microrotation field models transverse shearing and in-plane drilling rotations. We propose an incremental potential formulation of the Cosserat shell dynamics which allows for strong coupling with frictional contact and other physical systems. We evaluate a corresponding finite element discretization for non-planar shells using second-order elements which alleviates shear-locking and permits simulation of curved geometries. Our formulation and the discretization, in particular of the rotational degrees of freedom, is designed to integrate well with typical simulation approaches in physically-based animation. While the discretization of the rotations requires some care, we demonstrate that they do not pose significant numerical challenges in Newton’s method. In our experiments we also show that the codimensional shell model is consistent with the respective three-dimensional model. We qualitatively compare our formulation with Kirchhoff-Love shells and demonstrate intriguing use cases for the additional modes of control over dynamic deformations offered by the Cosserat model such as directly prescribing rotations or angular velocities and influencing the shell’s curvature.

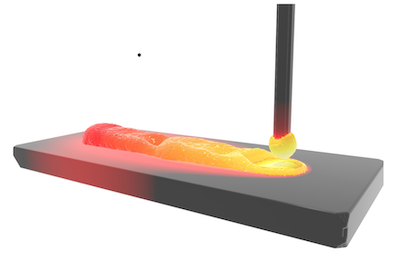
Cold metal transfer (CMT) is a variant of gas metal arc welding (GMAW) in which the molten metal of the wire is transferred to the weld pool mainly in the short-circuit phase. A special feature here is that the wire is retracted during this strongly controlled welding process. This allows precise and spatter-free formation of the weld seams with lower energy input. To simulate this process, a model based on the particle-based smoothed particle hydrodynamics (SPH) method is developed. This method provides a native solution for the mass and heat transfer. A simplified surrogate model was implemented as an arc heat source for welding simulation. This welding simulation model based on smoothed particle hydrodynamics method was augmented with surface effects, the Joule heating of the wire, and the effect of the electromagnetic forces. The model of metal transfer in the cold metal transfer process shows good qualitative agreement with real experiments.

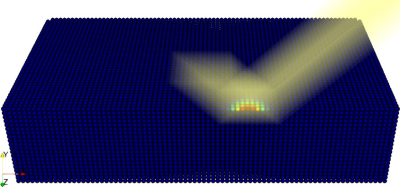
An important prerequisite for process simulations of laser beam welding is the accurate depiction of the surface energy distribution. This requires capturing the optical effects of the laser beam occurring at the free surface. In this work, a novel optics ray tracing scheme is proposed which can handle the reflection and absorption dynamics associated with laser beam welding. Showcasing the applicability of the approach, it is coupled with a novel surface detection algorithm based on smoothed particle hydrodynamics (SPH), which offers significant performance benefits over reconstruction-based methods. The results are compared to state-of-the-art experimental results in laser beam welding, for which an excellent correspondence in the case of the energy distributions inside capillaries is shown.