Publications

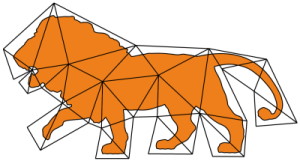
As demands for high-fidelity physics-based animations increase, the need for accurate methods for simulating deformable solids grows. While higher-order finite elements are commonplace in engineering due to their superior approximation properties for many problems, they have gained little traction in the computer graphics community. This may partially be explained by the need for finite element meshes to approximate the highly complex geometry of models used in graphics applications. Due to the additional per-element computational expense of higher-order elements, larger elements are needed, and the error incurred due to the geometry mismatch eradicates the benefits of higher-order discretizations. One solution to this problem is the embedding of the geometry into a coarser finite element mesh. However, to date there is no adequate, practical computational framework that permits the accurate embedding into higher-order elements.

We develop a novel, robust quadrature generation method that generates theoretically guaranteed high-quality sub-cell integration rules of arbitrary polynomial accuracy. The number of quadrature points generated is bounded only by the desired degree of the polynomial, independent of the embedded geometry. Additionally, we build on recent work in the Finite Cell Method (FCM) community so as to tackle the severe ill-conditioning caused by partially filled elements by adapting an Additive-Schwarz-based preconditioner so that it is suitable for use with state-of-the-art non-linear material models from the graphics literature. Together these two contributions constitute a general-purpose framework for embedded simulation with higher-order finite elements.

We finally demonstrate the benefits of our framework in several scenarios, in which second-order hexahedra and tetrahedra clearly outperform their first-order counterparts.

In this paper, we present a novel method for the robust handling of static and dynamic rigid boundaries in Smoothed Particle Hydrodynamics (SPH) simulations. We build upon the ideas of the density maps approach which has been introduced recently by Koschier and Bender. They precompute the density contributions of solid boundaries and store them on a spatial grid which can be efficiently queried during runtime. This alleviates the problems of commonly used boundary particles, like bumpy surfaces and inaccurate pressure forces near boundaries. Our method is based on a similar concept but we precompute the volume contribution of the boundary geometry. This maintains all benefits of density maps but offers a variety of advantages which are demonstrated in several experiments. Firstly, in contrast to the density maps method we can compute derivatives in the standard SPH manner by differentiating the kernel function. This results in smooth pressure forces, even for lower map resolutions, such that precomputation times and memory requirements are reduced by more than two orders of magnitude compared to density maps. Furthermore, this directly fits into the SPH concept so that volume maps can be seamlessly combined with existing SPH methods. Finally, the kernel function is not baked into the map such that the same volume map can be used with different kernels. This is especially useful when we want to incorporate common surface tension or viscosity methods that use different kernels than the fluid simulation.

Visually appealing and vivid simulations of deformable solids represent an important aspect of physically based computer animation. For the temporal discretization, it is customary in computer animation to use first-order accurate integration methods, such as Backward Euler, due to their simplicity and robustness. Although there is notable research on second-order methods, their use is not widespread. Many of these well-known methods have significant drawbacks such as severe numerical damping or scene-dependent time step restrictions to ensure stability. In this paper, we discuss the most relevant requirements on such methods in computer animation and motivate the interest beyond first-order accuracy. Keeping these requirements in mind, we investigate several promising methods from the families of diagonally implicit Runge-Kutta (DIRK) and Rosenbrock methods which currently do not appear to have considerable popularity in this field. We show that the usage of such methods improves the visual quality of physical animations. In addition, we demonstrate that they allow distinctly more control over damping at lower computational cost than classical methods. As part of our theoretical contribution, we review aspects of simulations that are often considered more intricate with higher-order methods, such as contact handling. To this end, we derive an implicit linearized contact model based on a predictor-corrector approach that leads to consistent behavior with higher-order integrators as predictors. Our contact model is well suited for the simulation of stiff, nonlinear materials with the integration methods presented in this paper and more common methods such as Backward Euler alike.