Publications

We present a strong fluid-rigid coupling for SPH fluids and rigid bodies with particle-sampled surfaces. The approach interlinks the iterative pressure update at fluid particles with a second SPH solver that computes artificial pressure at rigid body particles. The introduced SPH rigid body solver models rigid-rigid contacts as artificial density deviations at rigid body particles. The corresponding pressure is iteratively computed by solving a global formulation which is particularly useful for large numbers of rigid-rigid contacts. Compared to previous SPH coupling methods, the proposed concept stabilizes the fluid-rigid interface handling. It significantly reduces the computation times of SPH fluid simulations by enabling larger time steps. Performance gain factors of up to 58 compared to previous methods are presented. We illustrate the flexibility of the presented fluid-rigid coupling by integrating it into DFSPH, IISPH and a recent SPH solver for highly viscous fluids. We further show its applicability to a recent SPH solver for elastic objects. Large scenarios with up to 90M particles of various interacting materials and complex contact geometries with up to 90k rigid-rigid contacts are shown. We demonstrate the competitiveness of our proposed rigid body solver by comparing it to Bullet.

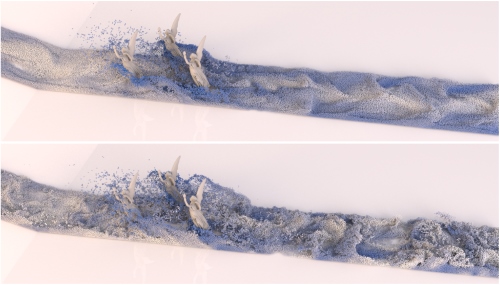
In this paper we introduce a novel micropolar material model for the simulation of turbulent inviscid fluids. The governing equations are solved by using the concept of Smoothed Particle Hydrodynamics (SPH). As already investigated in previous works, SPH fluid simulations suffer from numerical diffusion which leads to a lower vorticity, a loss in turbulent details and finally in less realistic results. To solve this problem we propose a micropolar fluid model. The micropolar fluid model is a generalization of the classical Navier-Stokes equations, which are typically used in computer graphics to simulate fluids. In contrast to the classical Navier-Stokes model, micropolar fluids have a microstructure and therefore consider the rotational motion of fluid particles. In addition to the linear velocity field these fluids also have a field of microrotation which represents existing vortices and provides a source for new ones. However, classical micropolar materials are viscous and the translational and the rotational motion are coupled in a dissipative way. Since our goal is to simulate turbulent fluids, we introduce a novel modified micropolar material for inviscid fluids with a non-dissipative coupling. Our model can generate realistic turbulences, is linear and angular momentum conserving, can be easily integrated in existing SPH simulation methods and its computational overhead is negligible. Another important visual feature of turbulent liquids is foam. Therefore, we present a post-processing method which considers microrotation in the foam particle generation. It works completely automatic and requires only one user-defined parameter to control the amount of foam.

Graphics research on Smoothed Particle Hydrodynamics (SPH) has produced fantastic visual results that are unique across the board of research communities concerned with SPH simulations. Generally, the SPH formalism serves as a spatial discretization technique, commonly used for the numerical simulation of continuum mechanical problems such as the simulation of fluids, highly viscous materials, and deformable solids. Recent advances in the field have made it possible to efficiently simulate massive scenes with highly complex boundary geometries on a single PC. Moreover, novel techniques allow to robustly handle interactions among various materials. As of today, graphics-inspired pressure solvers, neighborhood search algorithms, boundary formulations, and other contributions often serve as core components in commercial software for animation purposes as well as in computer-aided engineering software.

This tutorial covers various aspects of SPH simulations. Governing equations for mechanical phenomena and their SPH discretizations are discussed. Concepts and implementations of core components such as neighborhood search algorithms, pressure solvers, and boundary handling techniques are presented. Implementation hints for the realization of SPH solvers for fluids, elastic solids, and rigid bodies are given. The tutorial combines the introduction of theoretical concepts with the presentation of actual implementations.

In this paper, we present a novel method for the robust handling of static and dynamic rigid boundaries in Smoothed Particle Hydrodynamics (SPH) simulations. We build upon the ideas of the density maps approach which has been introduced recently by Koschier and Bender. They precompute the density contributions of solid boundaries and store them on a spatial grid which can be efficiently queried during runtime. This alleviates the problems of commonly used boundary particles, like bumpy surfaces and inaccurate pressure forces near boundaries. Our method is based on a similar concept but we precompute the volume contribution of the boundary geometry and store it on a grid. This maintains all benefits of density maps but offers a variety of advantages which are demonstrated in several experiments. Firstly, in contrast to the density maps method we can compute derivatives in the standard SPH manner by differentiating the kernel function. This results in smooth pressure forces, even for lower map resolutions, such that precomputation times and memory requirements are reduced by more than two orders of magnitude compared to density maps. Furthermore, this directly fits into the SPH concept so that volume maps can be seamlessly combined with existing SPH methods. Finally, the kernel function is not baked into the map such that the same volume map can be used with different kernels. This is especially useful when we want to incorporate common surface tension or viscosity methods that use different kernels than the fluid simulation.

Incompressible SPH (ISPH) is a promising concept for the pressure computation in SPH. It works with large timesteps and the underlying pressure Poisson equation (PPE) can be solved very efficiently. Still, various aspects of current ISPH formulations can be optimized.

This paper discusses issues of the two standard source terms that are typically employed in PPEs, i.e. density invariance (DI) and velocity divergence (VD). We show that the DI source term suffers from significant artificial viscosity, while the VD source term suffers from particle disorder and volume loss.

As a conclusion of these findings, we propose a novel source term handling. A first PPE is solved with the VD source term to compute a divergence-free velocity field with minimized artificial viscosity. To address the resulting volume error and particle disorder, a second PPE is solved to improve the sampling quality. The result of the second PPE is used for a particle shift (PS) only. The divergence-free velocity field - computed from the first PPE - is not changed, but only resampled at the updated particle positions. Thus, the proposed source term handling incorporates velocity divergence and particle shift (VD+PS).