Profile

Dynamics simulation with frictional contacts is important for a wide range of applications, from cloth simulation to object manipulation. Recent methods using smoothed lagged friction forces have enabled robust and differentiable simulation of elastodynamics with friction. However, the resulting frictional behavior can be inaccurate and may not converge to analytic solutions. Here we evaluate the accuracy of lagged friction models in comparison with implicit frictional contact systems. We show that major inaccuracies near the stick-slip threshold in such systems are caused by lagging of friction forces rather than by smoothing the Coulomb friction curve. Furthermore, we demonstrate how systems involving implicit or lagged friction can be correctly used with higher-order time integration and highlight limitations in earlier attempts. We demonstrate how to exploit forward-mode automatic differentiation to simplify and, in some cases, improve the performance of the inexact Newton method. Finally, we show that other complex phenomena can also be simulated effectively while maintaining smoothness of the entire system. We extend our method to exhibit stick-slip frictional behavior and preserve volume on compressible and nearly-incompressible media using soft constraints.

We explore micropolar materials for the simulation of volumetric deformable solids. In graphics, micropolar models have only been used in the form of one-dimensional Cosserat rods, where a rotating frame is attached to each material point on the one-dimensional centerline. By carrying this idea over to volumetric solids, every material point is associated with a microrotation, an independent degree of freedom that can be coupled to the displacement through a material's strain energy density. The additional degrees of freedom give us more control over bending and torsion modes of a material. We propose a new orthotropic micropolar curvature energy that allows us to make materials stiff to bending in specific directions.

For the simulation of dynamic micropolar deformables we propose a novel incremental potential formulation with a consistent FEM discretization that is well suited for the use in physically-based animation. This allows us to easily couple micropolar deformables with dynamic collisions through a contact model inspired from the Incremental Potential Contact (IPC) approach. For the spatial discretization with FEM we discuss the challenges related to the rotational degrees of freedom and propose a scheme based on the interpolation of angular velocities followed by quaternion time integration at the quadrature points.

In our evaluation we validate the consistency and accuracy of our discretization approach and demonstrate several compelling use cases for micropolar materials. This includes explicit control over bending and torsion stiffness, deformation through prescription of a volumetric curvature field and robust interaction of micropolar deformables with dynamic collisions.

We present a new octree-based neighborhood search method for SPH simulation. A speedup of up to 1.9x is observed in comparison to state-of-the-art methods which rely on uniform grids. While our method focuses on maximizing performance in fixed-radius SPH simulations, we show that it can also be used in scenarios where the particle support radius is not constant thanks to the adaptive nature of the octree acceleration structure.

Neighborhood search methods typically consist of an acceleration structure that prunes the space of possible particle neighbor pairs, followed by direct distance comparisons between the remaining particle pairs. Previous works have focused on minimizing the number of comparisons. However, in an effort to minimize the actual computation time, we find that distance comparisons exhibit very high throughput on modern CPUs. By permitting more comparisons than strictly necessary, the time spent on preparing and searching the acceleration structure can be reduced, yielding a net positive speedup. The choice of an octree acceleration structure, instead of the uniform grid typically used in fixed-radius methods, ensures balanced computational tasks. This benefits both parallelism and provides consistently high computational intensity for the distance comparisons. We present a detailed account of high-level considerations that, together with low-level decisions, enable high throughput for performance-critical parts of the algorithm.

Finally, we demonstrate the high performance of our algorithm on a number of large-scale fixed-radius SPH benchmarks and show in experiments with a support radius ratio up to 3 that our method is also effective in multi-resolution SPH simulations.

We propose a novel implicit density projection approach for hybrid Eulerian/Lagrangian methods like FLIP and APIC to enforce volume conservation of incompressible liquids. Our approach is able to robustly recover from highly degenerate configurations and incorporates volume-conserving boundary handling. A problem of the standard divergence-free pressure solver is that it only has a differential view on density changes. Numerical volume errors, which occur due to large time steps and the limited accuracy of pressure projections, are invisible to the solver and cannot be corrected. Moreover, these errors accumulate over time and can lead to drastic volume changes, especially in long-running simulations or interactive scenarios. Therefore, we introduce a novel method that enforces constant density throughout the fluid. The density itself is tracked via the particles of the hybrid Eulerian/Lagrangian simulation algorithm. To achieve constant density, we use the continuous mass conservation law to derive a pressure Poisson equation which also takes density deviations into account. It can be discretized with standard approaches and easily implemented into existing code by extending the regular pressure solver. Our method enables us to relax the strict time step and solver accuracy requirements of a regular solver, leading to significantly higher performance. Moreover, our approach is able to push fluid particles out of solid obstacles without losing volume and generates more uniform particle distributions, which makes frequent particle resampling unnecessary. We compare the proposed method to standard FLIP and APIC and to previous volume correction approaches in several simulations and demonstrate significant improvements in terms of incompressibility, visual realism and computational performance.

We develop a new operator splitting formulation for the simulation of corotated linearly elastic solids with Smoothed Particle Hydrodynamics (SPH). Based on the technique of Kugelstadt et al. [KKB2018] originally developed for the Finite Element Method (FEM), we split the elastic energy into two separate terms corresponding to stretching and volume conservation, and based on this principle, we design a splitting scheme compatible with SPH. The operator splitting scheme enables us to treat the two terms separately, and because the stretching forces lead to a stiffness matrix that is constant in time, we are able to prefactor the system matrix for the implicit integration step. Solid-solid contact and fluid-solid interaction is achieved through a unified pressure solve. We demonstrate more than an order of magnitude improvement in computation time compared to a state-of-the-art SPH simulator for elastic solids.

We further improve the stability and reliability of the simulation through several additional contributions. We introduce a new implicit penalty mechanism that suppresses zero-energy modes inherent in the SPH formulation for elastic solids, and present a new, physics-inspired sampling algorithm for generating high-quality particle distributions for the rest shape of an elastic solid. We finally also devise an efficient method for interpolating vertex positions of a high-resolution surface mesh based on the SPH particle positions for use in high-fidelity visualization.

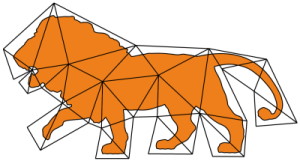
As demands for high-fidelity physics-based animations increase, the need for accurate methods for simulating deformable solids grows. While higher-order finite elements are commonplace in engineering due to their superior approximation properties for many problems, they have gained little traction in the computer graphics community. This may partially be explained by the need for finite element meshes to approximate the highly complex geometry of models used in graphics applications. Due to the additional per-element computational expense of higher-order elements, larger elements are needed, and the error incurred due to the geometry mismatch eradicates the benefits of higher-order discretizations. One solution to this problem is the embedding of the geometry into a coarser finite element mesh. However, to date there is no adequate, practical computational framework that permits the accurate embedding into higher-order elements.

We develop a novel, robust quadrature generation method that generates theoretically guaranteed high-quality sub-cell integration rules of arbitrary polynomial accuracy. The number of quadrature points generated is bounded only by the desired degree of the polynomial, independent of the embedded geometry. Additionally, we build on recent work in the Finite Cell Method (FCM) community so as to tackle the severe ill-conditioning caused by partially filled elements by adapting an Additive-Schwarz-based preconditioner so that it is suitable for use with state-of-the-art non-linear material models from the graphics literature. Together these two contributions constitute a general-purpose framework for embedded simulation with higher-order finite elements.

We finally demonstrate the benefits of our framework in several scenarios, in which second-order hexahedra and tetrahedra clearly outperform their first-order counterparts.

Visually appealing and vivid simulations of deformable solids represent an important aspect of physically based computer animation. For the temporal discretization, it is customary in computer animation to use first-order accurate integration methods, such as Backward Euler, due to their simplicity and robustness. Although there is notable research on second-order methods, their use is not widespread. Many of these well-known methods have significant drawbacks such as severe numerical damping or scene-dependent time step restrictions to ensure stability. In this paper, we discuss the most relevant requirements on such methods in computer animation and motivate the interest beyond first-order accuracy. Keeping these requirements in mind, we investigate several promising methods from the families of diagonally implicit Runge-Kutta (DIRK) and Rosenbrock methods which currently do not appear to have considerable popularity in this field. We show that the usage of such methods improves the visual quality of physical animations. In addition, we demonstrate that they allow distinctly more control over damping at lower computational cost than classical methods. As part of our theoretical contribution, we review aspects of simulations that are often considered more intricate with higher-order methods, such as contact handling. To this end, we derive an implicit linearized contact model based on a predictor-corrector approach that leads to consistent behavior with higher-order integrators as predictors. Our contact model is well suited for the simulation of stiff, nonlinear materials with the integration methods presented in this paper and more common methods such as Backward Euler alike.