Publications
An Optimized Source Term Formulation for Incompressible SPH

Incompressible SPH (ISPH) is a promising concept for the pressure computation in SPH. It works with large timesteps and the underlying pressure Poisson equation (PPE) can be solved very efficiently. Still, various aspects of current ISPH formulations can be optimized.
This paper discusses issues of the two standard source terms that are typically employed in PPEs, i.e. density invariance (DI) and velocity divergence (VD). We show that the DI source term suffers from significant artificial viscosity, while the VD source term suffers from particle disorder and volume loss.
As a conclusion of these findings, we propose a novel source term handling. A first PPE is solved with the VD source term to compute a divergence-free velocity field with minimized artificial viscosity. To address the resulting volume error and particle disorder, a second PPE is solved to improve the sampling quality. The result of the second PPE is used for a particle shift (PS) only. The divergence-free velocity field - computed from the first PPE - is not changed, but only resampled at the updated particle positions. Thus, the proposed source term handling incorporates velocity divergence and particle shift (VD+PS).
@Article{Cornelis2019,
author = {Cornelis, Jens and Bender, Jan and Gissler, Christoph and Ihmsen, Markus and Teschner, Matthias},
title = {An optimized source term formulation for incompressible SPH},
journal = {The Visual Computer},
year = {2019},
month = {Apr},
volume={35},
number={4},
pages={579--590},
issn = {1432-2315},
day = {20},
doi = {10.1007/s00371-018-1488-8},
url = {https://doi.org/10.1007/s00371-018-1488-8},
}
A Physically Consistent Implicit Viscosity Solver for SPH Fluids
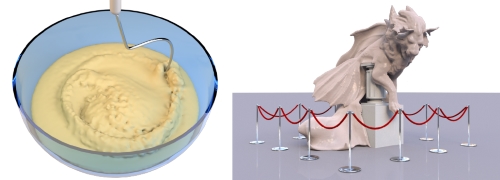
In this paper, we present a novel physically consistent implicit solver for the simulation of highly viscous fluids using the Smoothed Particle Hydrodynamics (SPH) formalism. Our method is the result of a theoretical and practical in-depth analysis of the most recent implicit SPH solvers for viscous materials. Based on our findings, we developed a list of requirements that are vital to produce a realistic motion of a viscous fluid. These essential requirements include momentum conservation, a physically meaningful behavior under temporal and spatial refinement, the absence of ghost forces induced by spurious viscosities and the ability to reproduce complex physical effects that can be observed in nature. On the basis of several theoretical analyses, quantitative academic comparisons and complex visual experiments we show that none of the recent approaches is able to satisfy all requirements. In contrast, our proposed method meets all demands and therefore produces realistic animations in highly complex scenarios. We demonstrate that our solver outperforms former approaches in terms of physical accuracy and memory consumption while it is comparable in terms of computational performance. In addition to the implicit viscosity solver, we present a method to simulate melting objects. Therefore, we generalize the viscosity model to a spatially varying viscosity field and provide an SPH discretization of the heat equation.
@article{WKBB2018,
author = {Marcel Weiler and Dan Koschier and Magnus Brand and Jan Bender},
title = {A Physically Consistent Implicit Viscosity Solver for SPH Fluids},
year = {2018},
journal = {Computer Graphics Forum (Eurographics)},
volume = {37},
number = {2}
}
Divergence-Free SPH for Incompressible and Viscous Fluids

In this paper we present a novel Smoothed Particle Hydrodynamics (SPH) method for the efficient and stable simulation of incompressible fluids. The most efficient SPH-based approaches enforce incompressibility either on position or velocity level. However, the continuity equation for incompressible flow demands to maintain a constant density and a divergence-free velocity field. We propose a combination of two novel implicit pressure solvers enforcing both a low volume compression as well as a divergence-free velocity field. While a compression-free fluid is essential for realistic physical behavior, a divergence-free velocity field drastically reduces the number of required solver iterations and increases the stability of the simulation significantly. Thanks to the improved stability, our method can handle larger time steps than previous approaches. This results in a substantial performance gain since the computationally expensive neighborhood search has to be performed less frequently. Moreover, we introduce a third optional implicit solver to simulate highly viscous fluids which seamlessly integrates into our solver framework. Our implicit viscosity solver produces realistic results while introducing almost no numerical damping. We demonstrate the efficiency, robustness and scalability of our method in a variety of complex simulations including scenarios with millions of turbulent particles or highly viscous materials.
@article{Bender2017,
author = {Jan Bender and Dan Koschier},
title = {Divergence-Free SPH for Incompressible and Viscous Fluids},
year = {2017},
journal = {IEEE Transactions on Visualization and Computer Graphics},
publisher = {IEEE},
year={2017},
volume={23},
number={3},
pages={1193-1206},
keywords={Smoothed Particle Hydrodynamics;divergence-free fluids;fluid simulation;implicit integration;incompressibility;viscous fluids},
doi={10.1109/TVCG.2016.2578335},
ISSN={1077-2626}
}
A Micropolar Material Model for Turbulent SPH Fluids

In this paper we introduce a novel micropolar material model for the simulation of turbulent inviscid fluids. The governing equations are solved by using the concept of Smoothed Particle Hydrodynamics (SPH). As already investigated in previous works, SPH fluid simulations suffer from numerical diffusion which leads to a lower vorticity, a loss in turbulent details and finally in less realistic results. To solve this problem we propose a micropolar fluid model. The micropolar fluid model is a generalization of the classical Navier-Stokes equations, which are typically used in computer graphics to simulate fluids. In contrast to the classical Navier-Stokes model, micropolar fluids have a microstructure and therefore consider the rotational motion of fluid particles. In addition to the linear velocity field these fluids also have a field of microrotation which represents existing vortices and provides a source for new ones. However, classical micropolar materials are viscous and the translational and the rotational motion are coupled in a dissipative way. Since our goal is to simulate turbulent fluids, we introduce a novel modified micropolar material for inviscid fluids with a non-dissipative coupling. Our model can generate realistic turbulences, is linear and angular momentum conserving, can be easily integrated in existing SPH simulation methods and its computational overhead is negligible.
@INPROCEEDINGS{Bender2017,
author = {Jan Bender and Dan Koschier and Tassilo Kugelstadt and Marcel Weiler},
title = {A Micropolar Material Model for Turbulent SPH Fluids},
booktitle = {Proceedings of the 2017 ACM SIGGRAPH/Eurographics Symposium on Computer
Animation},
year = {2017},
publisher = {ACM}
}
Density Maps for Improved SPH Boundary Handling

In this paper, we present the novel concept of density maps for robust handling of static and rigid dynamic boundaries in fluid simulations based on Smoothed Particle Hydrodynamics (SPH). In contrast to the vast majority of existing approaches, we use an implicit discretization for a continuous extension of the density field throughout solid boundaries. Using the novel representation we enhance accuracy and efficiency of density and density gradient evaluations in boundary regions by computationally efficient lookups into our density maps. The map is generated in a preprocessing step and discretizes the density contribution in the boundary's near-field. In consequence of the high regularity of the continuous boundary density field, we use cubic Lagrange polynomials on a narrow-band structure of a regular grid for discretization. This strategy not only removes the necessity to sample boundary surfaces with particles but also decouples the particle size from the number of sample points required to represent the boundary. Moreover, it solves the ever-present problem of particle deficiencies near the boundary. In several comparisons we show that the representation is more accurate than particle samplings, especially for smooth curved boundaries. We further demonstrate that our approach robustly handles scenarios with highly complex boundaries and even outperforms one of the most recent sampling based techniques.
@InProceedings{KB17,
author = {Dan Koschier and Jan Bender},
title = {Density Maps for Improved SPH Boundary Handling},
booktitle = {Proceedings of the 2017 ACM SIGGRAPH/Eurographics Symposium on Computer Animation},
year = {2017},
series = {SCA '17},
pages = {1--10},
publisher = {ACM}
}
Projective Fluids

We present a new method for particle based fluid simulation, using a combination of Projective Dynamics and Smoothed Particle Hydrodynamics (SPH). The Projective Dynamics framework allows the fast simulation of a wide range of constraints. It offers great stability through its implicit time integration scheme and is parallelizable in large parts, so that it can make use of modern multi core CPUs. Yet existing work only uses Projective Dynamics to simulate various kinds of soft bodies and cloth. We are the first ones to incorporate fluid simulation into the Projective Dynamics framework. Our proposed fluid constraints are derived from SPH and seamlessly integrate into the existing method. Furthermore, we adapt the solver to handle the constantly changing constraints that appear in fluid simulation. We employ a highly parallel matrix-free conjugate gradient solver, and thus do not require expensive matrix factorizations.
@inproceedings{Weiler2016,
author = {Marcel Weiler and Dan Koschier and Jan Bender},
title = {Projective Fluids},
booktitle = {Proceedings of ACM SIGGRAPH Conference on Motion in Games},
series = {MIG '16},
year = {2016},
publisher = {ACM}
}
Divergence-Free Smoothed Particle Hydrodynamics

In this paper we introduce an efficient and stable implicit SPH method for the physically-based simulation of incompressible fluids. In the area of computer graphics the most efficient SPH approaches focus solely on the correction of the density error to prevent volume compression. However, the continuity equation for incompressible flow also demands a divergence-free velocity field which is neglected by most methods. Although a few methods consider velocity divergence, they are either slow or have a perceivable density fluctuation.
Our novel method uses an efficient combination of two pressure solvers which enforce low volume compression (below 0.01%) and a divergence-free velocity field. This can be seen as enforcing incompressibility both on position level and velocity level. The first part is essential for realistic physical behavior while the divergence-free state increases the stability significantly and reduces the number of solver iterations. Moreover, it allows larger time steps which yields a considerable performance gain since particle neighborhoods have to be updated less frequently. Therefore, our divergence-free SPH (DFSPH) approach is significantly faster and more stable than current state-of-the-art SPH methods for incompressible fluids. We demonstrate this in simulations with millions of fast moving particles.
@INPROCEEDINGS{Bender2015,
author = {Jan Bender and Dan Koschier},
title = {Divergence-Free Smoothed Particle Hydrodynamics},
booktitle = {Proceedings of the 2015 ACM SIGGRAPH/Eurographics Symposium on Computer
Animation},
year = {2015},
publisher = {ACM},
doi = {http://dx.doi.org/10.1145/2786784.2786796}
}

