Publications

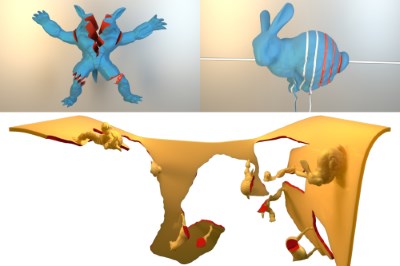
In this paper we present a robust remeshing-free cutting algorithm on the basis of the eXtended Finite Element Method (XFEM) and fully implicit time integration. One of the most crucial points of the XFEM is that integrals over discontinuous polynomials have to be computed on subdomains of the polyhedral elements. Most existing approaches construct a cut-aligned auxiliary mesh for integration. In contrast, we propose a cutting algorithm that includes the construction of specialized quadrature rules for each dissected element without the requirement to explicitly represent the arising subdomains. Moreover, we solve the problem of ill-conditioned or even numerically singular solver matrices during time integration using a novel algorithm that constrains non-contributing degrees of freedom (DOFs) and introduce a preconditioner that efficiently reuses the constructed quadrature weights. Our method is particularly suitable for fine structural cutting as it decouples the added number of DOFs from the cut's geometry and correctly preserves geometry and physical properties by accurate integration. Due to the implicit time integration these fine features can still be simulated robustly using large time steps. As opposed to this, the vast majority of existing approaches either use remeshing or element duplication. Remeshing based methods are able to correctly preserve physical quantities but strongly couple cut geometry and mesh resolution leading to an unnecessary large number of additional DOFs. Element duplication based approaches keep the number of additional DOFs small but fail at correct conservation of mass and stiffness properties. We verify consistency and robustness of our approach on simple and reproducible academic examples while stability and applicability are demonstrated in large scenarios with complex and fine structural cutting.

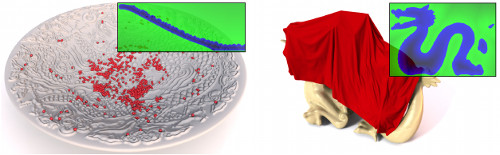
In this paper we present an hp-adaptive algorithm to generate discrete higher-order polynomial Signed Distance Fields (SDFs) on axis-aligned hexahedral grids from manifold polygonal input meshes. Using an orthonormal polynomial basis, we efficiently fit the polynomials to the underlying signed distance function on each cell. The proposed error-driven construction algorithm is globally adaptive and iteratively refines the SDFs using either spatial subdivision (h-refinement) following an octree scheme or by cell-wise adaption of the polynomial approximation's degree (p-refinement). We further introduce a novel decision criterion based on an error-estimator in order to decide whether to apply p- or h-refinement. We demonstrate that our method is able to construct more accurate SDFs at significantly lower memory consumption compared to previous approaches. While the cell-wise polynomial approximation will result in highly accurate SDFs, it can not be guaranteed that the piecewise approximation is continuous over cell interfaces. Therefore, we propose an optimization-based post-processing step in order to weakly enforce continuity. Finally, we apply our generated SDFs as collision detector to the physically-based simulation of geometrically highly complex solid objects in order to demonstrate the practical relevance and applicability of our method.

In this paper we present a novel Smoo­thed Particle Hy­dro­dy­na­mics (SPH) method for the efficient and stable simulation of incompressible fluids. The most efficient SPH-based approaches enforce incompressibility either on position or velocity level. However, the continuity equation for incompressible flow demands to maintain a constant density and a divergence-free velocity field. We propose a combination of two novel implicit pressure solvers enforcing both a low volume compression as well as a divergence-free velocity field. While a compression-free fluid is essential for realistic physical behavior, a divergence-free velocity field drastically reduces the number of required solver iterations and increases the stability of the simulation significantly. Thanks to the improved stability, our method can handle larger time steps than previous approaches. This results in a substantial performance gain since the computationally expensive neighborhood search has to be performed less frequently. Moreover, we introduce a third optional implicit solver to simulate highly viscous fluids which seamlessly integrates into our solver framework. Our implicit viscosity solver produces realistic results while introducing almost no numerical damping. We demonstrate the efficiency, robustness and scalability of our method in a variety of complex simulations including scenarios with millions of turbulent particles or highly viscous materials.

In this paper we introduce a novel micropolar material model for the simulation of turbulent inviscid fluids. The governing equations are solved by using the concept of Smoothed Particle Hydrodynamics (SPH). As already investigated in previous works, SPH fluid simulations suffer from numerical diffusion which leads to a lower vorticity, a loss in turbulent details and finally in less realistic results. To solve this problem we propose a micropolar fluid model. The micropolar fluid model is a generalization of the classical Navier-Stokes equations, which are typically used in computer graphics to simulate fluids. In contrast to the classical Navier-Stokes model, micropolar fluids have a microstructure and therefore consider the rotational motion of fluid particles. In addition to the linear velocity field these fluids also have a field of microrotation which represents existing vortices and provides a source for new ones. However, classical micropolar materials are viscous and the translational and the rotational motion are coupled in a dissipative way. Since our goal is to simulate turbulent fluids, we introduce a novel modified micropolar material for inviscid fluids with a non-dissipative coupling. Our model can generate realistic turbulences, is linear and angular momentum conserving, can be easily integrated in existing SPH simulation methods and its computational overhead is negligible.

In this paper, we present the novel concept of density maps for robust handling of static and rigid dynamic boundaries in fluid simulations based on Smoothed Particle Hydrodynamics (SPH). In contrast to the vast majority of existing approaches, we use an implicit discretization for a continuous extension of the density field throughout solid boundaries. Using the novel representation we enhance accuracy and efficiency of density and density gradient evaluations in boundary regions by computationally efficient lookups into our density maps. The map is generated in a preprocessing step and discretizes the density contribution in the boundary's near-field. In consequence of the high regularity of the continuous boundary density field, we use cubic Lagrange polynomials on a narrow-band structure of a regular grid for discretization. This strategy not only removes the necessity to sample boundary surfaces with particles but also decouples the particle size from the number of sample points required to represent the boundary. Moreover, it solves the ever-present problem of particle deficiencies near the boundary. In several comparisons we show that the representation is more accurate than particle samplings, especially for smooth curved boundaries. We further demonstrate that our approach robustly handles scenarios with highly complex boundaries and even outperforms one of the most recent sampling based techniques.

The physically-based simulation of mechanical effects has been an important research topic in computer graphics for more than two decades. Classical methods in this field discretize Newton's second law and determine different forces to simulate various effects like stretching, shearing, and bending of deformable bodies or pressure and viscosity of fluids, to mention just a few. Given these forces, velocities and finally positions are determined by a numerical integration of the resulting accelerations. In the last years position-based simulation methods have become popular in the graphics community. In contrast to classical simulation approaches these methods compute the position changes in each simulation step directly, based on the solution of a quasi-static problem. Therefore, position-based approaches are fast, stable and controllable which make them well-suited for use in interactive environments. However, these methods are generally not as accurate as force-based methods but provide visual plausibility. Hence, the main application areas of position-based simulation are virtual reality, computer games and special effects in movies and commercials. In this tutorial we first introduce the basic concept of position-based dynamics. Then we present different solvers and compare them with the variational formulation of the implicit Euler method in connection with compliant constraints. We discuss approaches to improve the convergence of these solvers. Moreover, we show how position-based methods are applied to simulate elastic rods, cloth, volumetric deformable bodies, rigid body systems and fluids. We also demonstrate how complex effects like anisotropy or plasticity can be simulated and introduce approaches to improve the performance. Finally, we give an outlook and discuss open problems.