Robust eXtended Finite Elements for Complex Cutting of Deformables

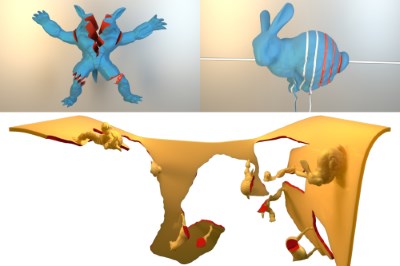
In this paper we present a robust remeshing-free cutting algorithm on the basis of the eXtended Finite Element Method (XFEM) and fully implicit time integration. One of the most crucial points of the XFEM is that integrals over discontinuous polynomials have to be computed on subdomains of the polyhedral elements. Most existing approaches construct a cut-aligned auxiliary mesh for integration. In contrast, we propose a cutting algorithm that includes the construction of specialized quadrature rules for each dissected element without the requirement to explicitly represent the arising subdomains. Moreover, we solve the problem of ill-conditioned or even numerically singular solver matrices during time integration using a novel algorithm that constrains non-contributing degrees of freedom (DOFs) and introduce a preconditioner that efficiently reuses the constructed quadrature weights. Our method is particularly suitable for fine structural cutting as it decouples the added number of DOFs from the cut's geometry and correctly preserves geometry and physical properties by accurate integration. Due to the implicit time integration these fine features can still be simulated robustly using large time steps. As opposed to this, the vast majority of existing approaches either use remeshing or element duplication. Remeshing based methods are able to correctly preserve physical quantities but strongly couple cut geometry and mesh resolution leading to an unnecessary large number of additional DOFs. Element duplication based approaches keep the number of additional DOFs small but fail at correct conservation of mass and stiffness properties. We verify consistency and robustness of our approach on simple and reproducible academic examples while stability and applicability are demonstrated in large scenarios with complex and fine structural cutting.