Publications

In this paper we present a novel operator splitting approach for corotated FEM simulations. The deformation energy of the corotated linear material model consists of two additive terms. The first term models stretching in the individual spatial directions and the second term describes resistance to volume changes. By formulating the backward Euler time integration scheme as an optimization problem, we show that the first term is invariant to rotations. This allows us to use an operator splitting approach and to solve both terms individually with different numerical methods. The stretching part is solved accurately with an optimization integrator, which can be done very efficiently because the system matrix is constant over time such that its Cholesky factorization can be precomputed. The volume term is solved approximately by using the compliant constraints method and Gauss-Seidel iterations. Further, we introduce the analytic polar decomposition which allows us to speed up the extraction of the rotational part of the deformation gradient and to recover inverted elements. Finally, this results in an extremely fast and robust simulation method with high visual quality that outperforms standard corotated FEMs by more than two orders of magnitude and even the fast but inaccurate PBD and shape matching methods by more than one order of magnitude without having their typical drawbacks. This enables a very efficient simulation of complex scenes containing more than a million elements.

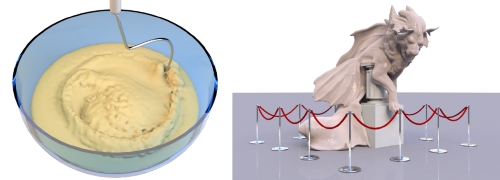
In this paper, we present a novel physically consistent implicit solver for the simulation of highly viscous fluids using the Smoothed Particle Hydrodynamics (SPH) formalism. Our method is the result of a theoretical and practical in-depth analysis of the most recent implicit SPH solvers for viscous materials. Based on our findings, we developed a list of requirements that are vital to produce a realistic motion of a viscous fluid. These essential requirements include momentum conservation, a physically meaningful behavior under temporal and spatial refinement, the absence of ghost forces induced by spurious viscosities and the ability to reproduce complex physical effects that can be observed in nature. On the basis of several theoretical analyses, quantitative academic comparisons and complex visual experiments we show that none of the recent approaches is able to satisfy all requirements. In contrast, our proposed method meets all demands and therefore produces realistic animations in highly complex scenarios. We demonstrate that our solver outperforms former approaches in terms of physical accuracy and memory consumption while it is comparable in terms of computational performance. In addition to the implicit viscosity solver, we present a method to simulate melting objects. Therefore, we generalize the viscosity model to a spatially varying viscosity field and provide an SPH discretization of the heat equation.

In this paper, we present a novel direct solver for the efficient simulation of stiff, inextensible elastic rods within the Position-Based Dynamics (PBD) framework. It is based on the XPBD algorithm, which extends PBD to simulate elastic objects with physically meaningful material parameters. XPBD approximates an implicit Euler integration and solves the system of non-linear equations using a non-linear Gauss-Seidel solver. However, this solver requires many iterations to converge for complex models and if convergence is not reached, the material becomes too soft. In contrast we use Newton iterations in combination with our direct solver to solve the non-linear equations which significantly improves convergence by solving all constraints of an acyclic structure (tree), simultaneously. Our solver only requires a few Newton iterations to achieve high stiffness and inextensibility. We model inextensible rods and trees using rigid segments connected by constraints. Bending and twisting constraints are derived from the well-established Cosserat model. The high performance of our solver is demonstrated in highly realistic simulations of rods consisting of multiple ten-thousand segments. In summary, our method allows the efficient simulation of stiff rods in the Position-Based Dynamics framework with a speedup of two orders of magnitude compared to the original XPBD approach.