Publications
Robust eXtended Finite Elements for Complex Cutting of Deformables
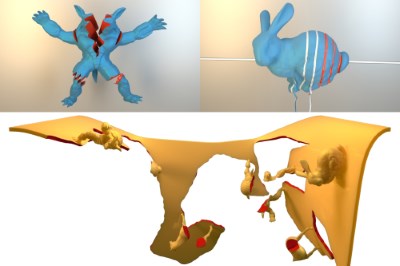
In this paper we present a robust remeshing-free cutting algorithm on the basis of the eXtended Finite Element Method (XFEM) and fully implicit time integration. One of the most crucial points of the XFEM is that integrals over discontinuous polynomials have to be computed on subdomains of the polyhedral elements. Most existing approaches construct a cut-aligned auxiliary mesh for integration. In contrast, we propose a cutting algorithm that includes the construction of specialized quadrature rules for each dissected element without the requirement to explicitly represent the arising subdomains. Moreover, we solve the problem of ill-conditioned or even numerically singular solver matrices during time integration using a novel algorithm that constrains non-contributing degrees of freedom (DOFs) and introduce a preconditioner that efficiently reuses the constructed quadrature weights. Our method is particularly suitable for fine structural cutting as it decouples the added number of DOFs from the cut's geometry and correctly preserves geometry and physical properties by accurate integration. Due to the implicit time integration these fine features can still be simulated robustly using large time steps. As opposed to this, the vast majority of existing approaches either use remeshing or element duplication. Remeshing based methods are able to correctly preserve physical quantities but strongly couple cut geometry and mesh resolution leading to an unnecessary large number of additional DOFs. Element duplication based approaches keep the number of additional DOFs small but fail at correct conservation of mass and stiffness properties. We verify consistency and robustness of our approach on simple and reproducible academic examples while stability and applicability are demonstrated in large scenarios with complex and fine structural cutting.
@ARTICLE{ Koschier2017,
author= {Dan Koschier and Jan Bender and Nils Thuerey},
title= {{Robust eXtended Finite Elements for Complex Cutting of Deformables}},
year= {2017},
journal= {ACM Transactions on Graphics (SIGGRAPH)},
publisher= {ACM},
volume = {36},
number = {4},
pages= {12}
}
Adaptive Tetrahedral Meshes for Brittle Fracture Simulation

We present a method for the adaptive simulation of brittle fracture of solid objects based on a novel reversible tetrahedral mesh refinement scheme. The refinement scheme preserves the quality of the input mesh to a large extent, it is solely based on topological operations, and does not alter the boundary, i.e. any geometric feature. Our fracture algorithm successively performs a stress analysis and increases the resolution of the input mesh in regions of high tensile stress. This results in an accurate location of crack origins without the need of a general high resolution mesh which would cause high computational costs throughout the whole simulation. A crack is initiated when the maximum tensile stress exceeds the material strength. The introduced algorithm then proceeds by iteratively recomputing the changed stress state and creating further cracks. Our approach can generate multiple cracks from a single impact but effectively avoids shattering artifacts. Once the tensile stress decreases, the mesh refinement is reversed to increase the performance of the simulation. We demonstrate that our adaptive method is robust, scalable and computes highly realistic fracture results.
@INPROCEEDINGS{Koschier2014,
author = {Dan Koschier and Sebastian Lipponer and Jan Bender},
title = {Adaptive Tetrahedral Meshes for Brittle Fracture Simulation},
booktitle = {Proceedings of the 2014 ACM SIGGRAPH/Eurographics Symposium on Computer
Animation},
year = {2014},
publisher = {Eurographics Association},
location = {Copenhagen, Denmark}
}

